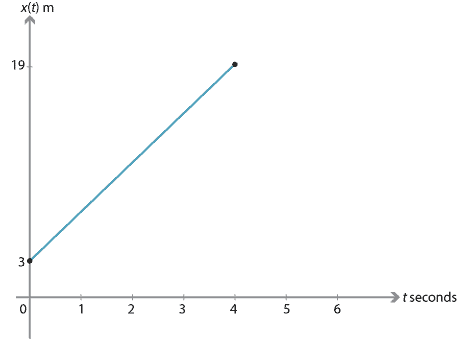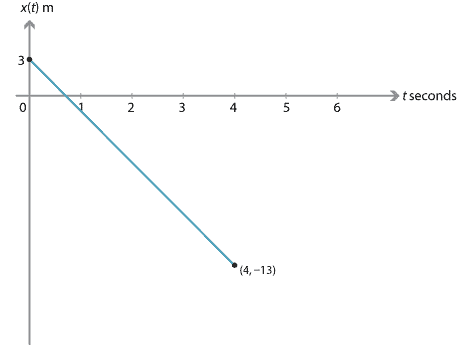Answers to exercises
Exercise 1
Exercise 2
From the first equation of motion, the velocity–time graph is given by \(v = u + at\). We assume \(u\) and \(v\) are positive.
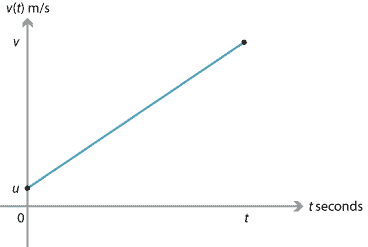
The displacement is equal to the area of the region under the velocity–time graph, which is a trapezium. So \(x = \dfrac{1}{2}(u+u+at)t = ut + \dfrac{1}{2}at^2\). This is the third equation of motion. If we substitute \(u = v-at\) into the third equation, we obtain the fifth equation.
Exercise 3
- \(v = 4.9 - 9.8t\) m/s.
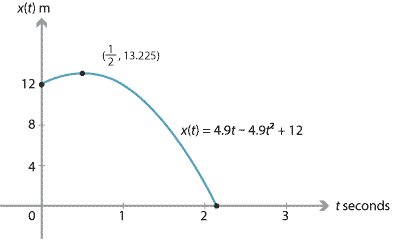
- \(x = 4.9t - 4.9t^2 + 12\) metres. (This is the position of the diver taking the origin to be the point on the water vertically below the diver's initial position.)
- Maximum height is reached when the velocity is zero. From the fourth equation of motion, we have \[ v^2 = 4.9^2 - 19.6d, \] where \(d\) is the displacement (that is, the position of the diver relative to the initial position). If \(v=0\), then \[ d = \dfrac{4.9^2}{19.6} = 1.225 \text{ metres}. \] Hence, the maximum height above the water is 13.225 metres.
- The diver reaches the water when \(x = 0\). This gives \(4.9t - 4.9t^2 + 12 = 0\), and therefore \(t = \dfrac{15}{7}\) seconds.
-
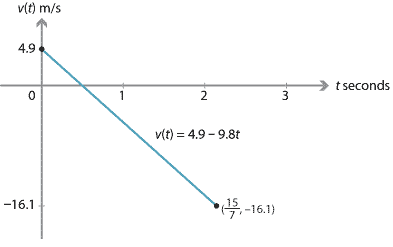
-
Exercise 4
Let \(h\) be the height of the tower. We measure positions from the base of the tower, taking the upwards direction as positive.
For the particle that initially goes up, we have \(x_{\mathrm{up}} = ut - \dfrac{1}{2}gt^2 + h\), and so
\[ 0 = ut_1 - \dfrac{1}{2}g(t_1)^2 + h, \qquad (1) \]where \(t_1\) is the time taken to reach the ground. For the particle that initially goes down, we have \(x_{\mathrm{down}} = -ut - \dfrac{1}{2}gt^2 + h\), and so
\[ 0 = -ut_2 - \dfrac{1}{2}g(t_2)^2 + h, \qquad (2) \]where \(t_2\) is the time taken to reach the ground.
We eliminate \(h\) by subtracting equation 2 from equation 1, and solve for \(u\):
\[ u = \dfrac{g}{2}\bigl(t_1-t_2\bigr). \]Substituting in equation 1 and solving for \(h\) gives
\[ h = \dfrac{g}{2}t_1t_2. \]For the particle dropped from the tower, we have \(x_{\mathrm{drop}} = -\dfrac{1}{2}gt^2 + h\). So
\[ 0 = -\dfrac{1}{2}gt^2 + h, \]where \(t\) is the time taken for the dropped particle to reach the ground. Substituting for \(h\) and solving for \(t\) gives \(t = \sqrt{t_1t_2}\).
Exercise 5
The two particles meet when \(-\dfrac{1}{2}gt^2 + h = ut - \dfrac{1}{2}gt^2\). Thus, the particles meet when
\[ h = ut. \qquad (1) \]When the dropped particle has travelled a distance of \(\dfrac{h}{n}\), we have
\[ -\dfrac{h}{n} = - \dfrac{1}{2}gt^2. \]Substitute for \(t\) from equation 1:
\[ -\dfrac{h}{n} = -\dfrac{g}{2}\Bigl(\dfrac{h}{u}\Bigr)^2. \]Now solve for \(u\):
\[ u = \sqrt{\dfrac{ngh}{2}}. \qquad (2) \]The ratio of the velocities is
\[ -gt : u-gt. \]Substituting from equation 1 and simplifying, this ratio is
\[ gh : gh-u^2. \]Now, substituting from equation 2 and simplifying, the ratio is
\[ 2 : 2-n. \]Exercise 6
39 metres.
Exercise 7
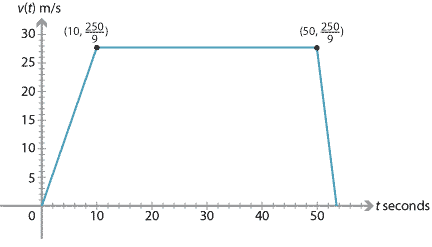
- 100 km/h \(= \dfrac{250}{9}\) m/s.
- The acceleration is \(\dfrac{25}{9}\) m/s\(^2\).
- The car travels 1288 metres.
- The car goes from 100 km/h to 0 km/h in 38 m. Thus \begin{align*} 0 &= \Bigl(\dfrac{250}{9}\Bigr)^2 + 2a \times 38 \\ a &= -\dfrac{15625}{1539} \text{ m/s}^2. \end{align*}
- \(\dfrac{342}{125}\) seconds.
-
Exercise 8
- \(\dot{x}(t)= (t-4)(3t-4)\).
- The particle is instantaneously at rest when \(\dot{x}(t) = 0\), so \(t = 4\) or \(t = \dfrac{4}{3}\).
- We have \(\ddot{x}(t)= 6t-16\), and so \(\ddot{x}(4) = 8\). The particle has an acceleration of 8 m/s\(^2\).
Exercise 9
- If \(x_A(t) = x_B(t)\), then \(3t^2 - 8t + 8 = 0\). The discriminant of \(3t^2 - 8t + 8\) is \(-32 < 0\). Thus there are no solutions, and the particles do not collide.
- The closest distance is \(\dfrac{2}{3}\).
- Over the time interval \([0,1)\), particle \(A\) is moving to the left and particle \(B\) to the right. Over \((2,\infty)\), particle \(A\) is moving to the right and particle \(B\) to the left.
Exercise 10
- \(\dfrac{1}{2 \pi}\)
- \(-\dfrac{1}{2 \pi}\)
- \(\dfrac{1}{\pi}\)